Không gian 4 chiều là gì? Ứng dụng của không gian 4 chiều vào thực tế

Không gian 4 chiều là gì?

Không gian 4 chiều hay còn gọi là không gian 4D là phần mở rộng toán học cho loại không gian 3 chiều (3D). Trước đó, người ta đã nhận định và thừa nhận rằng không gian là 3 chiều và được tạo bởi chiều dài (x) - chiều rộng (y) - chiều sâu (z). Joseph Louis Lagrange chính là người đã đưa thêm chiều thứ tư vào năm 1700 và 154 năm sau, Bernhard Riemann đưa ra kết quả chính xác cho không gian 4 chiều.

Năm 1880, Charles HowarD Hinton đã đưa ra bài luận mang tên “Chiều không gian thứ tư là gì”, trong đó có nêu ra những lý lẽ sâu sắc về không gian 4 chiều. Từ đó, thế giới có thể giải thích được rõ ràng hơn về không gian 4 chiều từ mô hình của một khối lập phương.

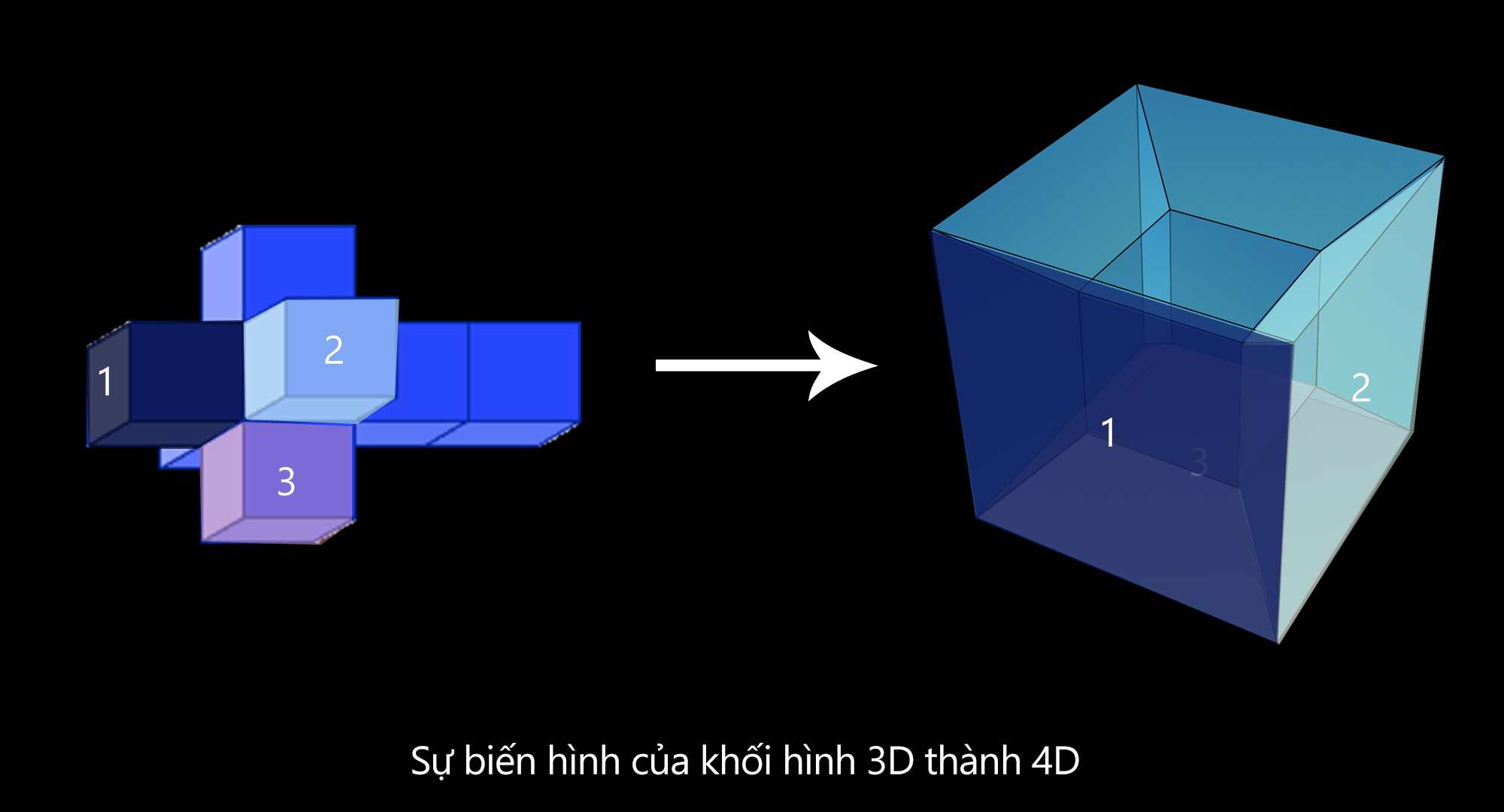
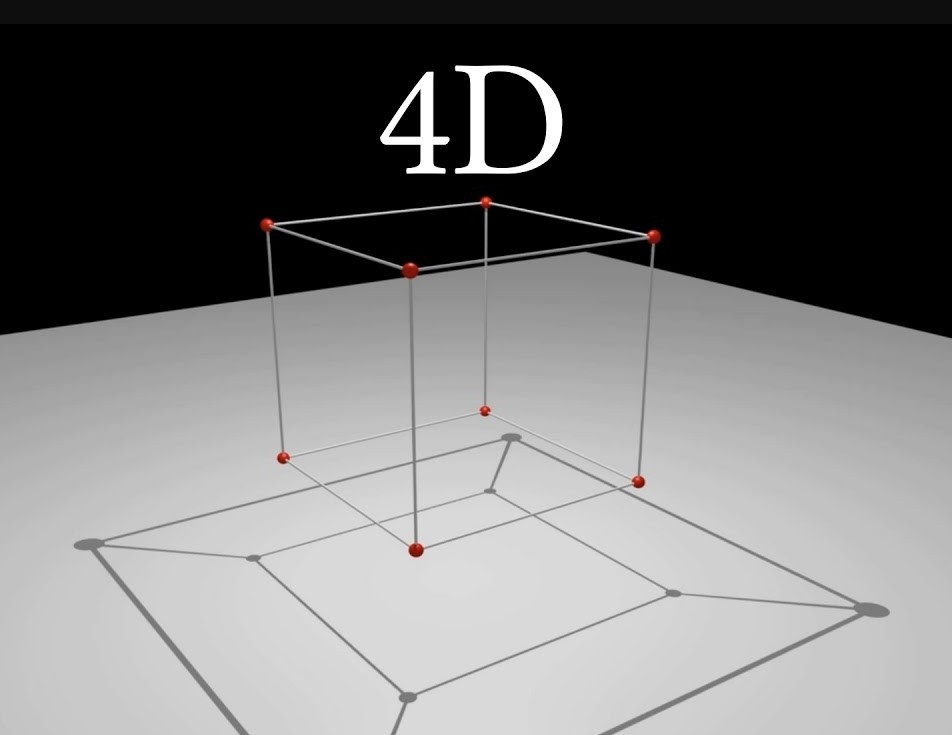
Hinton đã dùng hình thức đơn giản nhất để mọi người có thể hiểu được khái niệm này bằng cách vẽ hai khối hình nằm cách nhau trong khoảng “không nhìn thấy”, tiếp đến là vẽ hai khối hình nằm cách nhau ở khoảng “không nhìn thấy”, sau đó là vẽ cho nó đường giữa ở các đỉnh tương đương tạo ra 8 đường kết nối từ các đỉnh thuộc 2 khối hình này. Đây chính là đại diện cho một hướng duy nhất trong chiều không gian thứ 4 mà con người không thể nhìn thấy.

Qua những ý thuyết ở trên, người ta khẳng định không gian 4 chiều là một mô hình toán học được thiết lập từ 4 chiều được ký hiệu lần lượt là x, y, z, X. Không gian 4D này có những khối đa diện ở hình thức đa chiều, chiều thứ tư chính là chiều mở rộng của loại không gian 3 chiều và được ký hiệu là X. Không gian X là một trục vuông góc với toàn bộ trục còn lại, theo toán học thì nó chính là trục hoành (trục x theo toán học).

Những lập luận về không gian 4 chiều

Không gian 4 chiều ngoài cách gọi phổ biến là 4D thì còn được gọi là không gian đa chiều, nó trở thành một cơ sở quan trọng giúp con người thực hiện được những tính toán chính xác về mặt toán học và vật lý. Toán học, vật lý hay những lĩnh vực tương tự phần lớn đều cần phải dựa vào không gian 4 chiều mới có thể tồn tại được ở hình thức vốn có hiện tại của nó. Khái niệm không - thời gian của Einstein được đúng kết chính là nhờ việc dùng khái niệm không gian 4 chiều này mặc dù nó mang cấu trúc khá phức tạp - cấu trúc Minkowski, khó hình dung hơn nhiều so với loại không gian 4D Euclide.

Thực tế, đã có những kết luận được thừa nhận bởi các nhà khoa học rằng đường thẳng được tính là 1 chiều, mặt phẳng được tính là 2 chiều và không gian sẽ có 3 chiều. Ba yếu tố này được nhận diện bằng cách làm một trục tọa độ Oxyz, khi đó tất cả các điểm ở trong không gian đều được tọa độ này xác định rõ.

Khi nhắc tới chiều thứ tư, thường mọi người sẽ nghĩ đến chiều thời gian. Theo đó thì tất cả mọi điểm thuộc không gian thay vì thuộc tọa độ (x, y, z) thì sẽ thuộc tọa độ (x, y, z, t). Điều này dẫn tới kết quả một vị trí cố định thuộc tọa độ 3 điểm (x, y, z) sẽ chính là vô số các điểm thuộc không gian 4 chiều. Tọa độ của nó sẽ thay đổi theo t - được gọi là biến thời gian. Mặc dù 3 điểm x, y và z là cố định nhưng các điểm (x, y, z) của hôm nay sẽ không giống với điểm (x, y, z) của hôm trước, nguyên nhân vì t thay đổi từ hôm qua sang hôm nay.

Nếu như nhận định có chiều thứ 4 thì đồng nghĩa với việc đang nói đến số lượng “đại lượng tự do”. Số nhiều chính là số đại lượng tự do thuộc vào không gian đó, cũng có nghĩa là khi các nhà nghiên cứu muốn mô tả lại một không gian thì sẽ cần biến số tự do là bao nhiêu?

Do vậy, khi nhắc tới thuật ngữ không gian 4 chiều hoặc không gian nhiều chiều bất kỳ nghĩa là các nhà khoa học, toán học đang nhắc tới số lượng của một phạm trù gọi là “đại lượng tự do”. Số chiều, có thể là 2, 3 hoặc 4, tức là khi muốn mô tả không gian ấy thì các nhà nghiên cứu cần bao nhiêu “biến số tự do”.

Những ví dụ về không gian 4 chiều

Ví dụ tiêu biểu đầu tiên chính là vòng tròn. Nếu vòng tròn này có r=1 thì công thức được tính sẽ là x2 + y2 = 1.  Vòng tròn này sẽ thuộc mặt phẳng 2 chiều, xác định thông qua 2 biến số x và y. Lưu ý x và y không phải là những đại lượng tự do.

Theo điều kiện trên, khi ta cho x là một giá trị cụ thể thì y không tự do mà bắt buộc phải được tính bằng giá trị ±1-x2------√. Vì vậy, tuy vòng tròn thuộc mặt phẳng có 2 chiều thế nhưng bản thân vòng tròn lại chính là một vật thể 1 chiều.

Ví dụ thứ hai, đó là một mặt phẳng được tính theo công thức x+y+z=1. Đây là một mặt phẳng có 2 chiều nhưng trên thực tế nó nằm trong không gian 3 chiều vì phải cần tới 3 biến số mới có thể miêu tả được nó. Nhưng 3 biến số x, y và z không phải là tự do mà bằng 1-x-y. Trong đó, x và y là 2 đại lượng tự do, z phụ thuộc vào x và y.

Điều gì sẽ xảy ra khi bạn bước vào chiều không gian thứ 4?

Hiện tại, sau những học thuyết nhận định được đưa ra, con người đã nhận thức rất rõ về sự tồn tại của không gian 3 chiều: trên dưới, trái phải và trước sau. Để xác nhận sự tồn tại của chiều không gian thứ 4, nhân loại đã làm rất nhiều thí nghiệm. Các thí nghiệm này đều đưa chúng ta vào trong tưởng tượng về việc khi chúng ta bước vào không gian 4 chiều thì điều gì sẽ xảy ra?

Nhà khoa học sử dụng 2 thiết lập hai chiều, trong đó một thiết lập sẽ là các hạt nhẹ và thiết lập còn lại áp dụng với nguyên tử cực lạnh. Bằng phương pháp “giam” những electron vào trên một mặt phẳng 2D, tương tự như trên tờ giấy phẳng, tiếp đến là truyền từ trường đi qua tờ giấy này. Kết quả thu được là chiều không gian thứ 4 được nhìn thoáng qua dựa vào hiệu ứng Hall lượng tử. Trong khi trên thực tế, con người chỉ có thể nhận thức được đến không gian 3 chiều.

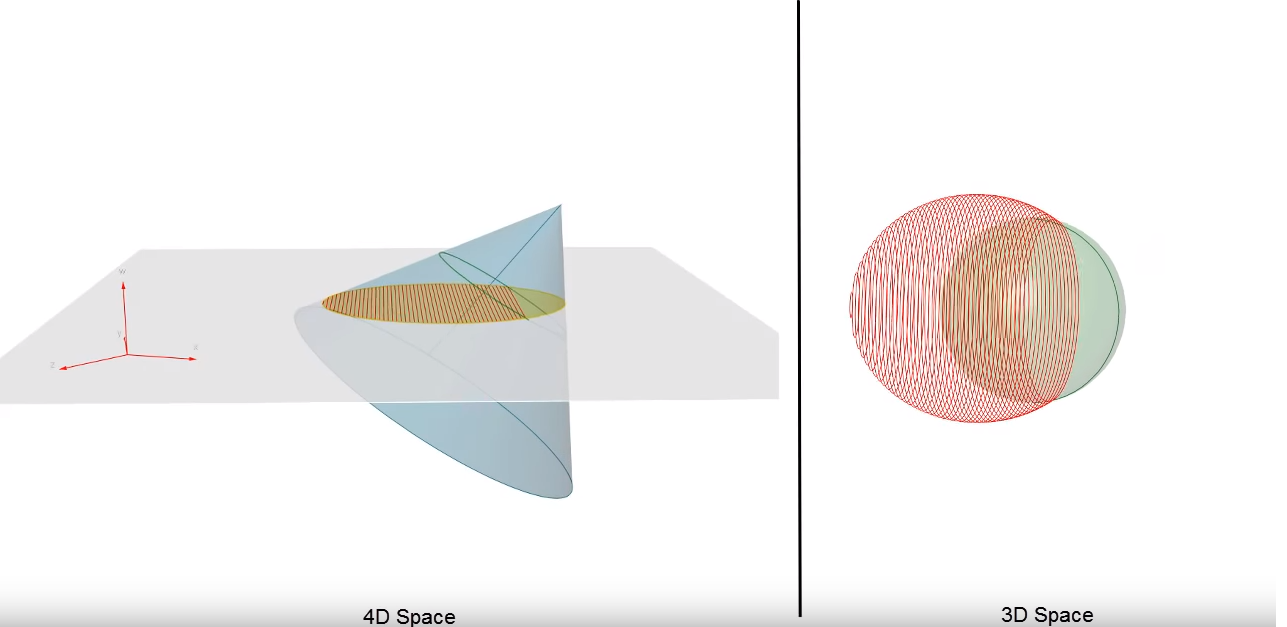
Thêm một ví dụ nữa có liên quan đến không gian 4 chiều đó là cái bóng. Thông thường một cái bóng chỉ tồn tại ở dạng 2 chiều. Qua quan sát cái bóng 2D, dễ dàng xác định được một vài tính chất của vật thể 3D khi chúng ta không quan sát trực tiếp. Tương tự đó, dù không quan sát được vật thể 4 chiều một cách trực tiếp nhưng ta vẫn có thể quan sát hiệu ứng của chiều thứ tư trong không gian 3 chiều, từ đó có thể khẳng định rằng không gian 4 chiều thực sự tồn tại.

Quan sát từ phương diện vật lý học, chúng ta sẽ không có không gian 4 chiều nhưng hoàn toàn có thể truy cập được vật lý Hall lượng tử 4D qua chiều thấp hơn bởi vì hệ thống chiều không gian cao hơn đã được mã hóa dựa trên mức độ phức tạp của cấu trúc.

Ứng dụng của không gian 4 chiều vào thực tế

Không gian 4 chiều chủ yếu xuất hiện trong toán học và vật lý. Đây là những lĩnh vực được các nhà khoa học dùng để truyền tải tri thức về thuyết không gian 4D đến nhân loại, giúp con người có thêm khả năng hình dung, liên tưởng gần hơn về thế giới xung quanh, từ đó có thể tham gia tìm kiếm và phát hiện thêm nhiều điều hữu ích khác. Ngoài ra, không gian 4 chiều đã được đưa vào ứng dụng trong cuộc sống hàng ngày, chẳng hạn như hình thức siêu âm 4D để soi được chi tiết những khu vực sâu bên trong cơ thể con người một cách rõ ràng, đem đến những hình dung cụ thể cho nền y học cũng như mỗi người bệnh.

Tổng kết

Việc hiểu không gian 4 chiều là gì không phải là chuyện đơn giản nhưng nếu nghiên cứu tìm hiểu sâu thì bạn sẽ thấy những điều thú vị từ không gian này. Hy vọng thông qua bài viết này quý bạn đọc sẽ có thêm hiểu hiểu về khái niệm cũng như ứng dụng của không gian 4 chiều trong cuộc sống, công việc.