Trả lời vấn đề: Thuộc tính nào sau đây là chất của tam giác?

Các tính chất cơ bản của tam giác

Thuộc tính nào sau đây là chất của tam giác? Để giải đáp cho vấn đề này, trước tiên ta cùng tìm hiểu về một số tính chất cơ bản của tam giác.

Toán học về tam giác có lượng kiến thức vô cùng phong phú, trong đó, tính chất của tam giác có rất nhiều. Chúng ta sẽ tìm hiểu lần lượt các tính chất đó để có thể nắm bắt kiến thức thật kỹ lưỡng, phục vụ cho việc học toán hiệu quả hơn.

Trước hết, phần những tính chất cơ bản, thuộc tính nào sau đây là chất của tam giác? Đó là:

• Tổng 3 góc của một tam giác bằng 180 độ.
• Số đo của góc ngoài tam giác bằng tổng số đo hai góc trong không kề với nó.

Đây là hai nội dung làm nên tính chất cơ bản của một tam giác mà bất cứ học sinh nào cũng phải nắm được trước khi giáo viên mở rộng, nâng cao thêm những tính chất đặc biệt khác về loại hình học này.

Một số tính chất "đặc biệt" trong tam giác

 Thuộc tính hay còn gọi là tính chất của tam giác, rất đa dạng. Thuộc tính nào sau đây là chất của tam giác? Cùng theo dõi những thông tin sau đây để biết thêm những kiến thức phong phú!

Tính chất về hai tam giác bằng nhau

Đôi khi giải toàn hình học liên quan đến tam giác, bạn sẽ bắt gặp những bài toán liên quan tới hai tam giác bằng nhau. Làm thế nào để học sinh có thể đưa ra được đáp án dễ dàng mà chính xác nhất? Muốn vậy, hãy cập nhập ngay những tính chất sau đây để áp dụng khi giải những bài toán dạng này nhé:

• Hai tam giác bằng nhau thì các cạnh tương ứng bằng nhau và các góc tương ứng của chúng cũng bằng nhau.
• Hai tam giác bằng nhau trường hợp cạnh - góc - cạnh: 2 cạnh bằng nhau và hai góc xen giữa của hai cạnh đó cũng bằng nhau.
• Hai tam giác bằng nhau trường hợp góc - cạnh - góc: 2 góc của hai tam giác bằng nhau và cạnh xen giữa hai góc đó cũng bằng nhau.
• Trường hợp bằng nhau cạnh - cạnh - cạnh của hai tam giác: 3 cạnh tương ứng cua hai tam giác này sẽ bằng nhau.
• Với 2 tam giác vuông, bằng nhau khi có 2 cạnh góc vuông, cạnh huyền góc nhọn, cạnh góc vuông và góc nhọn kề, cạnh huyền cạnh góc vuông tương ứng của chúng bằng nhau.

Tính chất tam giác cân, đều

Tiếp tục theo dõi thông tin để giải đáp vấn đề thuộc tính nào sau đây là chất của tam giác:

• Tam giác cân là tam giác có 2 cạnh bằng nhau, 2 góc bằng nhau.
• Tam giác đều có 2 cạnh bằng nhau, 3 góc bằng nhau và bằng 60 độ.
• Tam giác đều chính là tam giác cân với 1 góc có số đo bằng 60 độ.

Bất đẳng thức trong tam giác

Bất đẳng thức thường gặp trong tam giác đó là:

Trong một tam giác, 2 cạnh bất kỳ luôn có tổng lớn hơn và có hiệu luôn nhỏ hơn chiều dài cạnh còn lại.

Khi giải những bài toán liên quan đến bất đẳng thức trong tam giác, bạn có thể áp dụng tính chất này như một điều kiện hiển nhiên, đã được công nhận để làm bài. 

Tính chất các đường đặc biệt trong tam giác

Trong tam giác luôn tồn tại một số đường đặc biệt, mỗi đường đều có tính chất đặc trưng riêng. Khi giải toán về tam giác, bạn cần nhận diện những đường này để có thể dễ dàng áp dụng chúng tìm ra hướng giải cho cả bài. Cụ thể, tính chất của các đường đặc biệt trong tam giác có thể hiểu như sau:

• Đường cao là đường thẳng xuất phát từ đỉnh xuống và vuông góc với cạnh đối diện.
• Đường trung tuyến là đường thẳng nối từ đỉnh tam giác với trung điểm cạnh đối diện đỉnh đó.
• Đường trung trực của 1 cạnh tam giác là đường vuông góc tại trung điểm của cạnh đó.
• Đường trung bình là đường thẳng nối 2 trung điểm của 2 cạnh đối diện trong tam giác.
• Đường phân giác: đường thẳng chia một góc của tam giác ra thành hai góc có số đo bằng nhau.

Đặc biệt, 2 đường trung tuyến, 3 đường cao và 3 đường phân giác trong tam giác sẽ đồng quy tại một điểm.

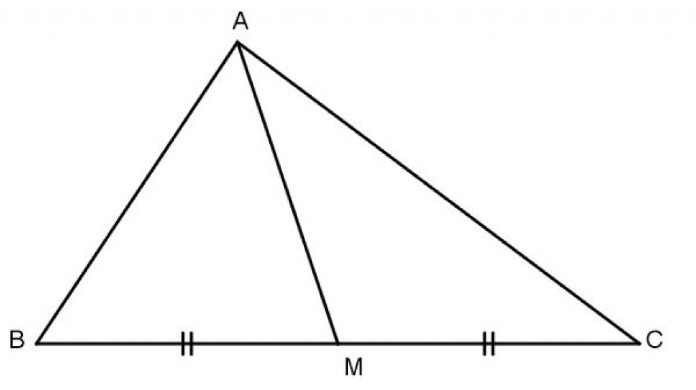
Tính chất cụ thể của tam giác cân và tam giác vuông cân

• Tính chất của tam giác cân

Trong một tam giác cân, hai góc đấy có độ lớn bằng nhau. Ví dụ: Tam giác ABC cân tại đỉnh A, từ đó suy ra góc ABC có số đo bằng góc ACB.

Một tam giác mà có hai góc bằng nhau sẽ là tam giác cân và cân tại đỉnh đối diện hai góc đó. Ví dụ: Tam giác AOB có góc OAB bằng góc OBA, suy ra tam giác OAB cân tại đỉnh O.

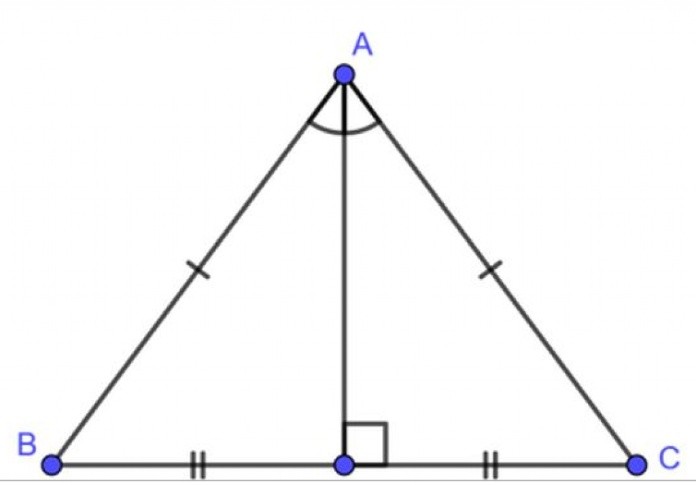
• Tính chất của tam giác vuông cân

Tam giác vuông cân là tam giác vuông đồng thời cũng là tam giác cân. Ở tam giác này sẽ có hai góc nhọn với độ lớn là 45 độ, 1 góc vuông và hai cạnh góc vuông bằng nhau. Với đặc điểm trê, tam giác vuông cân có những tính chất sau đây:

Tam giác vuông cân có hai góc đáy bằng nhau, bằng 45 độ.

Tam giác vuông cân có 3 đường gồm đường cao, đường phân giác tính từ đỉnh góc vuông và đường trung tuyến sẽ trùng nhau và 3 đường thẳng này có độ dài bằng nửa cạnh huyền.

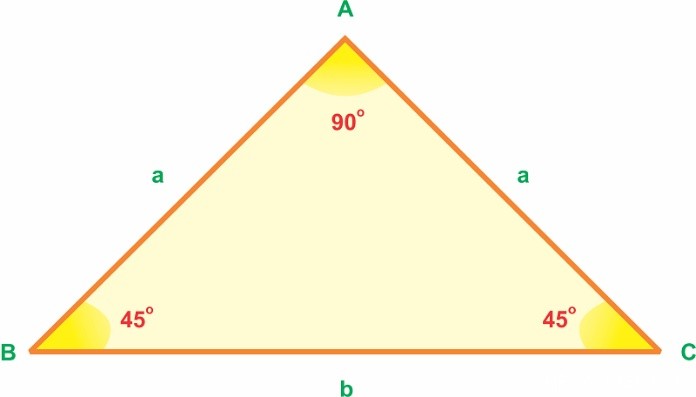
Các định lý trong tam giác

Tiếp theo đây là một số định lý trong tam giác giúp bạn làm rõ vấn đề thuộc tính nào sau đây là chất của tam giác, hãy cùng theo dõi nhé!

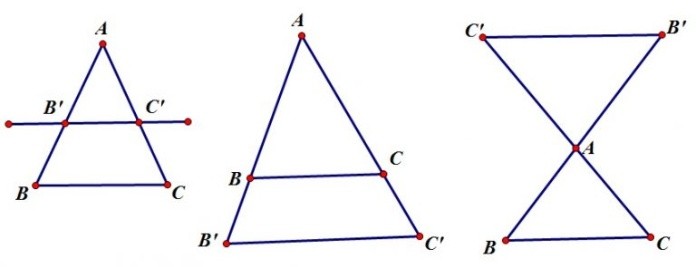
Định lý Talet trong tam giác

Định lý Talet bao gồm những nội dung quan trọng như sau:

Trong một tam giác, nếu một cạnh của tam giác song song với một đường thẳng thì đường thẳng này sẽ định ra trên 2 cạnh còn lại của tam giác đó những đoạn thẳng tương ứng tỉ lệ với nhau.

Nếu một đường thẳng định trên 2 cạnh của một tam giác những đoạn thẳng tương ứng tỉ lệ thì chắc chắn đường thẳng này song song với cạnh còn lại của tam giác đó. 

Nếu có đường thẳng cắt 2 cạnh trong tam giác và đồng thời song song với cạnh còn lại của tam giác đó thì sẽ tạo ra một tam giác mới có ba cạnh tương ứng tỉ lệ với ba cạnh của tam giác đầu tiên. 

Định lý cosin

Định lý cosin được hiểu như sau, trong một tam giác ABC bất kỳ giải sử số đo BC=a, CA=b và AB=C, ta có: 

• a^2 = b^2 + c^2 – 2b.c. cos A
• b^2 = a^2 + c^2 – 2a.c. cos B
• c^2 = a^2 + b^2 – 2a.b. cos C

Định lý sin

Trong tam giác ABC bất kỳ với BC = a, CA = b, AB = c, và R là bán kính đường tròn ngoại tiếp tam giác ABC. Định lý sin được biểu diễn như sau:

a/sinA = b/sinB = c/sinc =2R

Lời kết

Thông qua bài viết trên, chúng tôi đã giải đáp chi tiết nhất cho bạn đọc về câu hỏi thuộc tính nào sau đây là chất của tam giác. Phương pháp để bạn có thể nắm bắt được những thuộc tính này đó là thường xuyên áp dụng và giải nhiều bài tập. Chúc các bạn có thể nâng cao kiến thức toán học của mình qua những nội dung chia sẻ qua bài viết này nhé.