Tổng quan kiến thức và dạng bài tập hình học không gian 11
Hình học không gian là gì?
Hình học không gian chắc hẳn không còn xa lạ với học sinh trung học phổ thông.
Những kiến thức cơ bản về hình học không gian lớp 11
Để vẽ được hình biểu diễn của một hình không gian thì ta dựa vào những quy tắc sau:
- Hình biểu diễn của đường thẳng là đường thẳng, tương ứng của đoạn thẳng thì là đoạn thẳng.
- Hình biểu diễn của hai đường thẳng song song là hai đường thẳng song song, tương tự với hai đường thẳng cắt nhau là 2 đường thẳng cắt nhau.
- Hình biểu diễn phải giữ nguyên quan hệ giữa điểm với đường thẳng.
- Dùng nét vẽ liền để biểu diễn những đường nhìn thấy và dùng nét đứt để vẽ các đường bị che khuất.
Quan hệ song song
Hai mặt phẳng song song khi đáp ứng yêu cầu không có điểm chung thì ta có 2 mặt phẳng đó song song với nhau.
- Nếu đường thẳng (α) chứa 2 đường thẳng cắt nhau là a, b và a, b cùng song song với mặt phẳng (β) thì (α) và (β) song song với nhau.
- Qua một điểm nằm bên ngoài mặt phẳng cho trước thì ta chỉ vẽ được một và chỉ một mặt phẳng song song với mặt phẳng đã cho.
- Cho 2 mặt phẳng song song với nhau. Nếu một mặt phẳng cắt mặt phẳng này thì cũng đồng thời cắt mặt phẳng kia và hai giao tuyến của chúng sẽ song song với nhau.
- Định lý Ta - let: ba mặt phẳng đôi một song song chắn trên 2 cát tuyến bất kỳ các đoạn tương ứng tỷ lệ.

Vector trong không gian
Vector trong không gian là đoạn thẳng có hướng nhất định. Vector được ký hiệu là → chỉ điểm đầu và điểm cuối của một đoạn thẳng.
Những quy tắc về việc sử dụng vector trong không gian bao gồm những quy tắc sau: 3 điểm, quy tắc hình bình hành, quy tắc trung điểm, quy tắc trung tuyến, quy tắc trọng tâm và quy tắc hình hộp. Tất cả các kiến thức về hình không gian chúng ta sẽ được giảng dạy trong sách giáo khoa hình học 11.
Điều kiện đồng phẳng của 3 vector: trong không gian 3 vector được gọi là đồng phẳng với nhau nếu giá của chúng cùng song song với một mặt phẳng bất kỳ.
Ví dụ về vector trong không gian như sau:
Cho tứ diện ABCD, gọi E và F lần lượt là những trung điểm của AB và CB. Chứng minh rằng 3 vector BC, AD, EF đồng phẳng với nhau.
Lời giải:
Gọi P và Q lần lượt là những trung điểm của AC và BD. Ta có PE // FQ và PE = FQ = ½ AD.
=> Tứ giác EFPQ là một hình bình hành.
(EFPQ) chứa đường thẳng EF đồng thời song song với đường thẳng AD và BC.
=> EF, AD, BC cùng song song với một mặt phẳng.
=> Ba vector BC, EF, AD đồng phẳng với nhau.
Quan hệ vuông góc
Trong bài tập về quan hệ vuông góc bạn cần hiểu được các kiến thức cơ bản về đường thẳng sẽ vuông góc với mặt phẳng khi nào? Các định nghĩa, tính chất cũng như lý thuyết chung của nó.
Cách chứng minh đường thẳng vuông góc với mặt phẳng và chứng chứng minh nó như sau:
Ví dụ: Tứ diện ABCD có 2 mặt, ACB và CBD là 2 tam giác cân có chung đáy là BC. Điểm I là trung điểm của BC. Chứng minh rằng:
- BC vuông góc với (ADI)
- Gọi AH là đường cao của △ACB và △CBD là 2 tam giác cân có chung đáy là BC. I là trung điểm của BC. Chứng minh rằng AH ⊥ (BCD)
Lời giải:
- Do tam giác ABC và BCD là hai tam giác cân tại A và D nên:
AI ⊥ BC
DI ⊥ BC
Trong tam giác cân đường trung tuyến đồng thời là đường cao
=> BC ⊥ (ADI)
- Vì AH là đường cao trong tam giá ADI nên AH ⊥ DI
Có BC ⊥ (ADI) => BC ⊥ AH
=> AH ⊥ (BCD)

Bài toán về góc
Đối với bài tập về góc cần phải xác định được những yếu tố về góc giữa 2 đường thẳng chéo nhau. Góc giữa đường thẳng và mặt phẳng, góc giữa cạnh bên và mặt đáy, cách tính góc giữa cạnh bên và mặt phẳng chứa đường cao, góc giữa đường cao và mặt bên, công thức, lý thuyết,... Tóm lại bài tập và kiến thức về hình học không gian rất rộng và bao la.
Những dạng bài tập hình học không gian 11 và lời giải hay
Những bài tập hình học không gian cũng rất phong phú và đa dạng và có nhiều lời giải hay. Dưới đây là một số dạng bài đặc trưng nhất cùng với lời giải đi kèm:
Bài toán: Bài tập về tìm giao tuyến của 2 mặt phẳng.
Cách giải:
- Tìm 2 điểm chung của 2 mặt phẳng này, điểm chung thứ nhất thường rất dễ tìm. Điểm chung thứ 2 thường là giao điểm của 2 đường thẳng còn lại, không qua điểm chung thứ nhất.
- Nếu trong 2 mặt phẳng có chứa 2 đường thẳng song song với nhau, ta chỉ cần tìm thêm một điểm chung nữa. Lúc này giao tuyến của nó sẽ đi qua điểm chung và song song với cả 2 đường thẳng này.
Ví dụ: Hình chóp S.ABCD có tam giác SBC lấy điểm M, trong tam giác SCD lấy điểm N. Tìm giao tuyến của (SMN) và (ABCD).
Lời giải:
Ở (SBC), gọi E= SM ∩ BC => E= (SMN) ∩ (ABCD)
Ở (SCD), gọi F= SN ∩ CD => F= (SMN) ∩ (ABCD)
=> EF= (SMN) ∩ (ABCD)
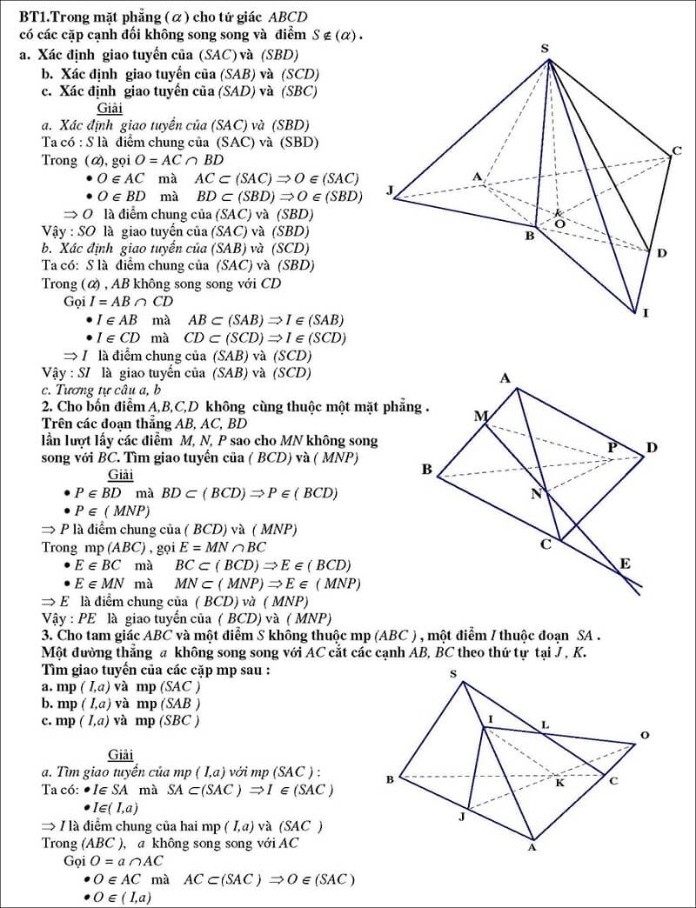
Cách học giỏi hình không gian lớp 11
Hình học không gian là phần tương đối phức tạp nên bạn cần nắm được một số bí quyết để có thể làm tốt ở phần này.
Biết cách tưởng tượng và vẽ hình chính xác là bước quan trọng đầu tiên
Trước khi bước vào giải bất cứ một bài tập hình học không gian nào thì bạn hãy chắc chắn rằng mình đã vẽ hình đúng nhất là việc hình nhìn thấy và hình bị che khuất. Nét nào được vẽ liền và nét nào phải vẽ bằng nét đứt.
Bạn nên xem xét thật kỹ yêu cầu đề bài nhằm xác định đúng dạng bài. Nhớ thuộc lòng những định lý, tính cách và hệ quả của nó để ứng dụng vào các dạng hình học khác nhau.

Luyện làm nhiều các dạng đề khác nhau để thành thạo
Học sinh cần rèn luyện và làm bài tập nhiều nhằm trau dồi khả năng cũng như biết nhiều dạng đề khác nhau.
Càng vẽ nhiều hình học không gian khác nhau, học sinh sẽ càng thành thạo và tưởng tượng và nắm bắt được nhiều khía cạnh khác nhau của vấn đề đưa ra trong bài tập hình học không gian.
Đầu tư công sức và thời gian cho việc làm bài tập và tham khảo nhiều dạng bài tập hình học không gian trên mạng
Sách giáo khoa và sách bài tập là các bài cơ bản về kiến thức và kỹ năng cho bản thân. Để có được các kiến thức nâng cao và chuẩn bị hành trang bước vào kỳ thi lớp 12 hay đại học thì bài tập hình học không gian lớp 11 là yếu tố quan trọng và cần thiết trong đề thi.
Dựa vào tính chất của những bài thi có sự linh hoạt và phân theo mức độ đánh giá năng lực cá nhân. Nên những bài thi này có sự phân hóa cao.

Lời kết
Mong rằng với những chia sẻ trên đây đã mang đến cho học sinh những kiến thức bổ ích liên quan tới hình học không gian. Qua các ví dụ được đưa ra này, hy vọng các bạn sẽ tự tin hơn khi làm bài.