Các cách chứng minh hình bình hành chuẩn không cần chỉnh

Hình bình hành là gì?

Trước khi đi vào chứng minh hình bình hành, bạn cần hiểu hình bình hành là gì. Trong tiếng anh, hình bình hành được gọi là Parallelogram, tức là một hình tứ giác có các cạnh đối song song. Trong sách giáo khoa lớp 4: hình bình hành là hình tứ giác đặc biệt có hai cặp cạnh đối song song và bằng nhau. Hình bình hành cũng là hình thang đặc biệt.

Ví dụ: Tứ giác ABCD được coi là hình bình hành khi  AB//DC, AD//BC; AB=DC, AD=BC

Cách nhận biết hình bình hành

Bạn có thể áp dụng những dấu hiệu nhận biết sau đây để chứng minh hình bình hành

• Tứ giác có hai cặp cạnh đối diện song song là hình bình hành
• Tứ giác có hai cặp cạnh đối diện bằng nhau là hình bình hành
• Tứ giác có một cặp cạnh vừa song song vừa bằng nhau là hình bình hành
• Tứ giác có các góc đối diện bằng nhau là hình bình hành
• Tứ giác có hai đường chéo cắt nhau tại trung điểm mỗi đường là hình bình hành.
• Hình thang có hai cạnh đáy bằng nhau là hình bình hành
• Hình thang có hai cạnh bên song song là hình bình hành

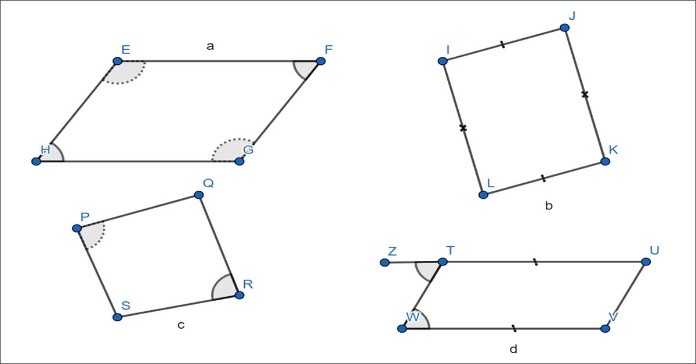
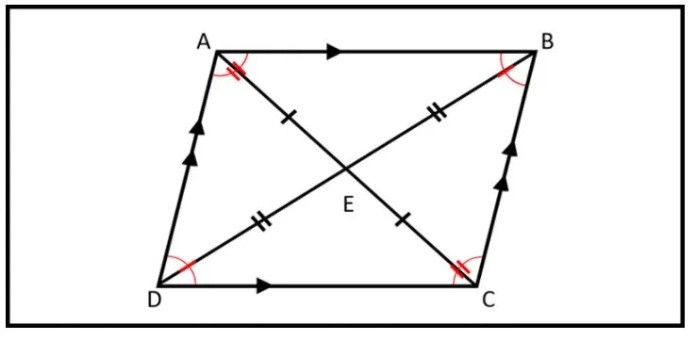
Tính chất của hình bình hành

Để chứng minh hình bình hành, bạn cần nắm rõ tính chất của nó. Có 3 tính chất cần nhớ là:

• Trong hình bình hành, các cạnh đối luôn song song và bằng nhau
• Trong hình bình hành, các góc đối sẽ bằng nhau
• Trong hình bình hành, hai đường chéo luôn cắt nhau tạo trung điểm mỗi đường

Hiểu được tính chất hình bình hành chính là yếu tố cơ bản để cm hình bình hành. Vì cm hình bình hành CDEF tức là chứng minh CDEF có các tính chất trên.

Một số phép tính liên quan đến hình bình hành

Diện tích hình bình hành bằng cạnh đáy nhân chiều cao:

S= c x h

(Trong đó S là diện tích, c là chiều dài cạnh đáy, h là chiều cao.)

Chu vi hình bình hành bằng hai lần tổng hai cạnh kề nhau:

C= 2x(a+b)

(Trong đó C là chu vi, a và b là hai cạnh kề nhau của hình bình hành.)

Để nhớ được công thức này, bạn có thể nhớ đoạn thơ sau: 

“Bình hành diện tích tính sao

Chiều cao nhân đáy ra liền khó chi.

Chu vi thì cần những gì

Cạnh kề cộng lại ta liền nhân hai.”

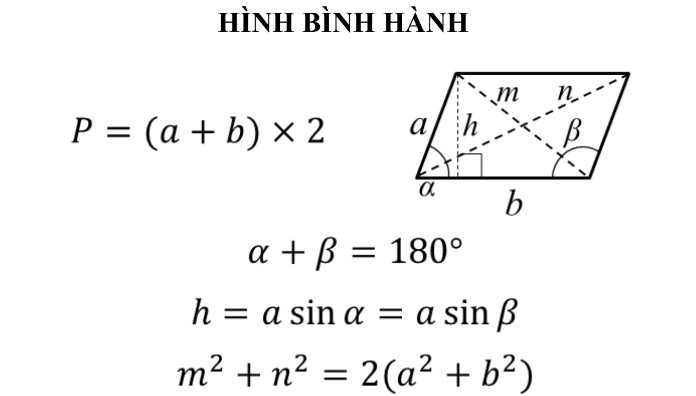
Các cách chứng minh hình bình hành

Trong hình bình hành thì chứng minh hbh. Để chứng minh tứ giác là hình bình hành, bạn cần dựa vào tính chất và dấu hiệu nhận biết của nó. Tùy vào dữ liệu đề bài mà chọn cách cm hình bình hành phù hợp. Có các cách chứng minh hình bình hành sau:

Cách một: chứng minh tứ giác đó có các cạnh đối song song

Để chứng minh tứ giác là hình bình hành, ta có thể tiến hành chứng minh tứ giác đó có các cạnh đối song song với nhau.

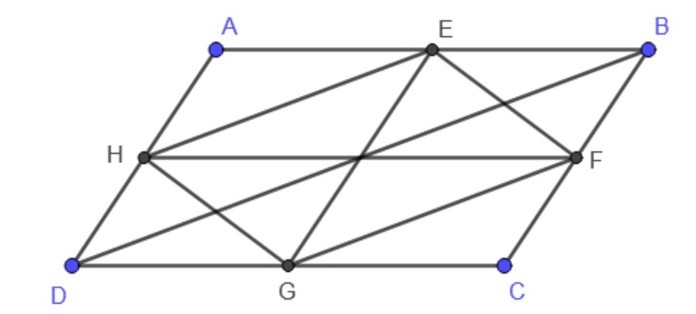
Ví dụ: Cho tứ giác ABCD, trong đó E là trung điểm của AB, F là trung điểm của BC, G là trung điểm của CD, H là trung điểm của DA. Chứng minh EFGH là hình bình hành

Ta có EF là đường trung bình của tam giác ABC => EF//AC

HG là đường trung bình của tam giác ACD => HG//AC

FG là đường trung bình của tam giác CBD => FG//BD

HE là đường trung bình của tam giác ABD => HE//BD

EF//HG; FG//HE

EFGH là hình bình hành vì có các cạnh đối song song với nhau

Cách hai: chứng minh tứ giác đó có các cạnh đối bằng nhau 

Đây cũng là một cách cm hình bình hành thường thấy. Theo đó, người học chứng minh tứ giác là hình bình hành khi tứ giác đó có các cạnh đối bằng nhau.

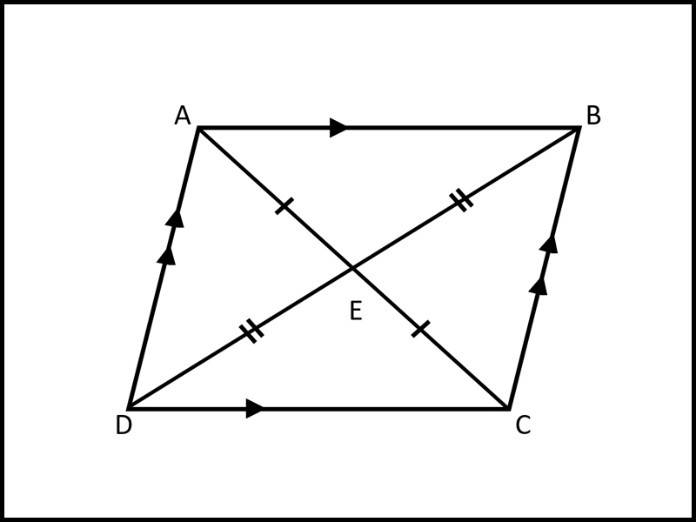
Ví dụ: Cho tứ giác ABCD có hai tam giác bằng nhau là ABC và CDA. Chứng minh ABCD là hình bình hành. 

Ta có: tam giác ABC = tam giác CDA

=> AB = CD, BC = DA => ABCD là hình bình hành vì có các cạnh đối bằng nhau

Cách ba: Chứng minh tứ giác có các cạnh đối song song và bằng nhau

Đây là cách chứng minh tứ giác là hình bình hành dựa trên tính chất hai cạnh đối song song và bằng nhau. Bạn có thể tham khảo ví dụ sau:

Ví dụ: Cho hình bình hành ABCD, trong đó E là trung điểm của AD, F là trung điểm của BC. Chứng minh BEDF là hình bình hành.

Ta có ABCd là hình bình hành => AD = BC, AD//BC

AD//BC => DE//BF

E là trung điểm AD => DE = AD/2 = BC/2

E là trung điểm BC => BF = BC/2

BEDF có hai cạnh đối song song bằng nhau => Là hình bình hành

Cách 4: Chứng minh tứ giác có các góc đối bằng nhau

Trong hình bình hành thì chứng minh hbh là chứng minh tứ giác có hai góc đối bằng nhau. Để hiểu rõ hơn, bạn hãy tham khảo ví dụ về cách chứng minh tứ giác là hình bình hành sau:

Ví dụ: Cho tứ giác ABCD, trong đó tam giác ABD = tam giác BCD, tam giác ABC = tam giác ADC. Chứng minh ABCD là hình bình hành

Ta có tam giác BCD = tam giác BAD => góc BCD = BAD

Tam giác ABC = tam giác ADC => góc ABC = góc ADC

ABCD có các góc đối bằng nhau => tứ giác ABCD là hình bình hành

Cách 5: Chứng minh tứ giác có hai đường chéo cắt nhau tại trung điểm 

Đây là một trong các cách chứng minh hình bình hành, sử dụng tính chất đường chéo trong hình bình hành luôn cắt nhau tại trung điểm. Cách cm hình bình hành này cũng vô cùng đơn giản. Hãy đến với ví dụ sau đây để hiểu hơn nhé

Ví dụ: Cho hình bình hành ABCD, AC và BD cắt nhau tại O. Từ A kẻ vuông góc tới BD, gọi là E; từ C kẻ vuông góc tới BD gọi là F. Chứng minh AECF là hình bình hành

Ta có OA = OC (vì ABCD là hình bình hành) (1)

Góc AEO = góc CFO = 90 độ 

Góc AOE = góc COF (đối đỉnh)

Tam giác AEO = tam giác CFO => OE =OF (2)

AECF là hình bình hành do hai đường chéo cắt nhau tại trung điểm mỗi đường

Một vài lưu ý khi chứng minh hình bình hành

Để việc chứng minh hình bình hành trở nên đơn giản hơn, hãy cùng đến với một vài lưu ý khi làm bài:

• Sau khi đọc đề, hãy vẽ hình ra giấy. Việc này giúp bạn hình dung nhanh chóng các cách chứng minh hình bình hành và lựa chọn được cách chứng minh phù hợp. Việc này còn giúp bạn tránh nhầm lẫn các hình với nhau. Ngoài ra, với nhiều thầy cô, nếu bạn không vẽ hình sẽ không có điểm.
• Vẽ được hình là bạn đã giải quyết được 50% bài toán. Sau đó hãy dựa vào các kiến thức để chứng minh tứ giác là hình bình hành.
• Đừng áp dụng lý thuyết quá máy móc mà hãy quan sát hình, trong hình bình hành thì chứng minh hbh, linh hoạt, sáng tạo, khoa học, trình bày các bước dựa vào hình vẽ giúp người đọc dễ hiểu, dễ hình dung.

Lời kết

Vừa rồi là tổng quan về hình bình hành và cách chứng minh hình bình hành. Hy vọng bài viết sẽ giúp bạn học tốt hơn và yêu thích hình học hơn. Nếu còn gì thắc mắc, hãy để lại bình luận để được giải đáp. Xin cảm ơn!